正規化の重要性‼

はじめに

この度、正規化を完全に理解したので、私なりに各正規形についてできるだけわかりやくすなるよう説明していきたいと思います。

正規化とは

正規化とは、データベースにおいて、データの無駄なところをなくして、異状が発生しないようにするために行われるもの。

正規化には、

• 非正規形
• 第１正規形
• 第２正規形
• 第３正規形
• ボイス・コッド正規形
• 第４正規形
• 第５正規形

があります。
（ほんとは第６正規形という概念もあるけど無駄でしかないと思えるものだし高度試験にも出ないしないよ）

前提知識：キー

正規化を説明する前に、キーについておさらい。

（ここではわかり易さ重視のため、属性を列、タプルを行と呼ぶこととします）

キーとは

表において、行を一意に識別するための列、または列の組み合わせ。

行を一意に識別できるなら、キーは複数の列の組み合わせでもいいのです。
なにも主キーは単一の列である必要はない！

候補キー

表中の行を一意に識別できる必要最小限の行の組み合わせ。
この「候補キー」は、表中に複数存在しうる。

例: {ユーザID}，{電話番号}など

ちなみに、この必要最小限の行の組み合わせのことを「極小」と呼んだりする。

主キー

そんな複数ある候補キーの中から、表中で一つだけ設定できる存在。

メインの識別子。

スーパーキー

表中の行を一意に識別できる列または列の組み合わせ。
まあつまりキー。
「主キー」「候補キー」と何が違うかというと、必要最小限の組み合わせである必要がない！

極小である必要がないのだ！

つまり、表中の行を一意に識別できるならいくつ列を組み合わせてもいいやつ、というわけだ。
その組み合わせに候補キーが一つでも入ってたらいいってことだな！

外部キー

ほかの表の主キーを参照する項目のこと。

非キー

どの候補キーの一部にも含まれない列のこと。

主キー、候補キー、スーパーキーの違い

例を挙げるのがわかり易いでしょう。

｛社員コード、社員名、電話番号、住所｝

という列をもつ表で考えてみます。

この表において、行を一意に識別できる列はどれでしょう。
｛社員コード｝と｛電話番号｝かな？｛社員名｝は人名なので被る可能性あるし。

となると、この表における候補キーは｛社員コード｝、｛電話番号｝となります。

次に主キー。
｛電話番号｝にNULLが入ってる行がありますね。それに｛電話番号｝は機種変更で変わる可能性もあります。
ならば主キーは｛社員コード｝にするのが妥当でしょう。

ここがポイントなのですが、候補キーはNULLを許可する列を含みます。主キーにはNULLは入れられない。
この制約をそれぞれ「一意性制約」、「主キー制約」と呼びます。

これが主キーと候補キーの一番の違いと言えるでしょう。

ちなみにSQLではそれぞれ「UNIQUE」、「PRIMARY KEY」で列に制約を付与できます。

最後にスーパーキー。

スーパーキーは、行を一意に識別できれば極小である必要がない。つまり

• ｛社員コード｝
• ｛社員コード，社員名｝
• ｛社員コード，電話番号｝
• ｛社員コード，住所｝
• ｛社員コード，社員名，電話番号｝
• ｛社員コード，社員名，住所｝
• ｛社員コード，電話番号、住所｝
• ｛社員コード，社員名，電話番号，住所｝
• ｛電話番号｝
• ｛電話番号，社員名｝
• ｛電話番号，住所｝
• ｛電話番号，社員名，住所｝

の組み合わせすべてがスーパーキーであるということ！
候補キーとの組み合わせ全部ですね。

サロゲートキー

ついでにサロゲートキーについても書いといちゃいます。

サロゲートキーは訳すと「代用キー」となります。
わかり易い例を挙げると、「連番」なんかですね。

主キーが複数の列からなってるのがよろしくないときに使うやつ。

非正規形

では正規化についての話を始めましょう。
まずは非正規形。

非正規形とは

「表の列の中に、単一でない値が含まれている」というもの。
いやわかりにくい。

とても噛み砕いて説明すると、スプレッドシートでいう「**セルの結合**」がある状態と捉えていい。
↓こんな感じの（行方向、列方向どちらでも）

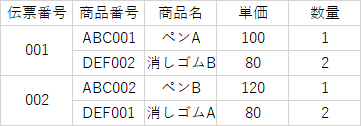
そもそも表というのは２次元のデータ構造。
でもセルの結合のような状態があったらどうだろう。
......それ３次元のデータにならないか？

なんか都合悪くなりそうな感じするわな。

第１正規形

そこでまずは第１正規形。

セルの結合をなくして単純な形にする！それだけ！

つまりこんな感じの表になる。

ちなみに、この表における主キーは｛伝票番号，商品番号｝になりますね。

第２正規形

つぎに第２正規形。
でもセルの結合は解除したよ。何するの

答えは「更新時異状を防止する形にする」。

更新時異状とは

第１正規形だとまだデータに無駄が多いんですよね。
それ故にデータ操作時に不具合が起こっちゃう。

たとえば、上の表で「消しゴムA」の名前を「すごい消しゴム」に変える必要が出てきたと考えてみましょう。
したらこの表の「消しゴムA」の箇所をすべて同時に変更する必要が出てきます。
......これ、もし更新中に障害が発生したりで１行でも変更しそびれたら、マズいっすよね。存在しないデータが発生してしまう。
これを特に「修正時異状」と呼びます。
ほかにも新規データ挿入時に発生する「挿入時異状」、
データ削除時に発生する「削除時異状」があります。

こういった異状を防止するために正規化というものを行います。

ここで正規化の必要性がわかったところで、さっそく第２正規形にしてみましょう。
第２正規形では、候補キーの一部に部分関数従属する非キーを別の表に分けます。

は？？？？

とりあえず部分関数従属について説明します

部分関数従属性

「候補キーの一部」なら、候補キーが単一の列の場合はどうなのか。
その場合は部分関数従属していない、といえます。

ちなみに、部分関数従属していない状態のことを完全関数従属と呼ぶ。

話を戻します。
第２正規形とは「すべての非キーが、どの候補キーにも部分関数従属していない」こと。

つまり、そもそも候補キーが単一の列の場合は既に第２正規形の条件を満たしている、ということでもある。

では、先ほどの表において部分関数従属しているところをあぶり出してみます。

候補キーは｛伝票番号，商品番号｝なので、｛伝票番号｝または｛商品番号｝のいずれかのみで値を決定できるところを探せばいいですね。

探してみると、｛商品番号｝のみから｛商品名｝と｛単価｝が決定できます。
ここで｛商品番号｝は候補キー｛伝票番号，商品番号｝の一部なので、部分関数従属しているといえます。
じゃ分解じゃ！

さあ、部分関数従属をなくしました。
これで第２正規形の条件を満たしました。やったね

第３正規形

ついに来ました第３正規形！
正規化は第３正規形までやることが基本なので、ここまでできれば十分！

でもこれ以上どうするんじゃ
......実は先ほどの表は第２正規化した時点で第３正規形の条件も満たしちゃってます。
なので、ここでは別の表を使って説明していきます。

まず主キーは｛伝票番号｝。
ほかに｛店舗ID｝→｛店舗名，住所｝の従属関係がありますが、行を一意に識別できるものではないため、候補キーではありません。非キーです。

一応第２正規形かどうかも確認しておきます。
そもそも候補キーが｛伝票番号｝の1つのみですので、第２正規形の条件を満たしています。

では第３正規形の話を始めましょう。
第３正規形では、推移的関数従属する非キーを別の表に分けます。

ここでまず推移的関数従属の説明をば

推移的関数従属性

ここでXは候補キー、
Y、Zは非キー。

名前の通りXからY、YからZへと推移的に従属している関係のことです。
ここで重要なのは、YからXへ従属していないという点。

第３正規形である条件は「すべての非キーが、いかなる候補キーにも推移的関数従属性していない」こと。

では、先の表を第３正規形にしていきます。

まず、この表における推移的関数従属してそうな列の関係を矢印で表してみます。
｛伝票番号｝→｛店舗ID｝→｛店舗名｝となっていることが読み取れるでしょうか。
また、｛店舗ID｝→｛伝票番号｝は成り立っていないですね。
つまりこれは推移的関数従属だ、といえます。
では分解

ヨシ！
......ん？
でもなんか｛店舗ID｝→｛店舗名｝→｛住所｝も推移的関数従属してそうじゃね？

ここで②の条件が重要になってくるのだ！
②の条件をこの関係に置き換えてみましょう。

①｛店舗ID｝→｛店舗名｝
②｛店舗名｝→｛店舗ID｝でない
③｛店舗名｝→｛住所｝

お？②がちょっとおかしいとは思いませんか？
常識的に考えて、店舗名が被ることはないでしょう。つまり一意性がある。
なら｛店舗名｝から｛店舗ID｝を決定できるのではないか、と

となると②の条件を満たせませんね。｛店舗名｝→｛店舗ID｝の従属関係が成り立ってしまっているから。
よってこれは推移的関数従属ではない。
つまり第３正規形の条件を満たしている！

第３正規化おわり！！！！

ボイス・コッド、第４、第５正規形について

ボイス・コッド正規形はギリ応用情報の試験範囲だけど、名前さえ知ってれば解ける程度の問題しか出ない。
第４正規形は高度試験にほんの数回出てきたことがあるだけ。
第５正規形は高度試験の解答例に出てくるだけ。

なのでここでの説明はいたしません。

そもそも第３正規形まででとどめておくのが実務的にも基本なので。

まとめ

情報処理技術者試験では、ある関係が示されて、それが第○正規形まで正規化されているか問われる問題が出題されることがあります。
したがって、各正規形について根拠をもって説明までできるようになるのが理想的です！

といってもやることは簡単で、いくつかの短い決まり文句を覚えてしまうだけです。
（詳しくは参考文献①を買ってあげてください……）

という訳で、ここでは各正規形の条件について簡単に復習して締めようかと思います。

各正規形の条件について復習

第１正規形

表中の全ての列が単一の値である。

わかり易い表現で言うと、セルの結合が存在しない。

２次元のデータ構造で表現できる。

※ただし、主キーを定められない場合は表を分ける。

第２正規形

第１正規形の条件を満たしており、
すべての非キーがどの候補キーにも部分関数従属していない。

｛A，B｝→｛C｝は成立するが
｛A｝→｛C｝または｛B｝→｛C｝が成立しない状態。

第３正規形

第２正規形の条件を満たしており、
すべての非キーがどの候補キーにも推移的関数従属していない。

「｛A｝→｛B｝→｛C｝は成立するが、
｛B｝→｛A｝は成立しない」という関係が<span class="bold">存在しない</span>状態。

こちらの記事ではわかり易さ重視のため、属性を列、タプルを行として扱いました。

厳密性を重視するならば属性、タプルと書くべきではあります。
どういうことかは、なぜ「表モデル」ではなく「関係モデル」なのか、など調べてみてもらえると。

おわりに

どうでしょう、ここまでできたら「正規化完全に理解した！」と思わず言っちゃうのではないでしょうか。
ここまで読んでくれてありがとう

参考文献

1. ITのプロ46『情報処理教科書 データベーススペシャリスト 2021年版』，翔泳社，2020年
2. 中山清喬，飯田理恵子『スッキリわかるSQL入門 第3版 ドリル256問付き!』，インプレス，2022年